I recently worked with a large set of accounting transactions. I needed to split those rows into multiple logical batches, but each batch had to be logically consistent – among other things, those batches had to be properly balanced, because accounting people are kind of fussy like that.

So I designed a little T-SQL logic that would split all of those transactions into evenly sized batches, without violating their logical groupings.

Safety glasses on. Let’s dive in.

Some test data

Let’s build ourselves some mock data. I’ll create a temp table called #rows, which will contain 10 000 rows. The exact number of groups will vary depending on what database you run this in, because the mock-up script uses sys.objects and sys.columns as a source.

DROP TABLE IF EXISTS #rows;

SELECT TOP (10000)
       o1.[object_id] AS grouping_column_1,
       o2.[object_id] AS grouping_column_2,
       c.column_id AS ordering_column
INTO #rows
FROM sys.objects AS o1
CROSS JOIN (SELECT TOP (10) [object_id] FROM sys.objects) AS o2
INNER JOIN sys.columns AS c ON o2.[object_id]=c.[object_id]
WHERE c.column_id<25;

CREATE UNIQUE CLUSTERED INDEX UCIX
    ON #rows (grouping_column_1, grouping_column_2, ordering_column);

Getting started

My aim with this post is to split the dataset into batches of roughly 100 rows each.

DECLARE @target_rowcount bigint=100;

I say “roughly”, because we’re not allowed to split a transaction so that a group (grouping_column_1, grouping_column_2) appears in more than one batch, although a batch can obviously contain more than one group. This means that by necessity, some of the batches are going to be slightly under 100 rows and some are going to be slightly over.

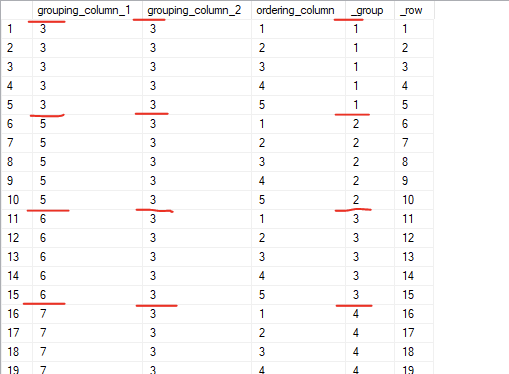
I’m going to approach the problem as a chained series of common table expressions. In the first CTE, we’ll define two temporary columns that we’ll need going forward: a sequential batch number and a “plain” row number for the entire dataset.

WITH step_1 AS (
    SELECT *,
           DENSE_RANK() OVER (
                ORDER BY grouping_column_1,
                         grouping_column_2) AS _group,
           ROW_NUMBER() OVER (
                ORDER BY grouping_column_1,
                         grouping_column_2,
                         ordering_column) AS _row
    FROM #rows)
    
SELECT * FROM step_1;

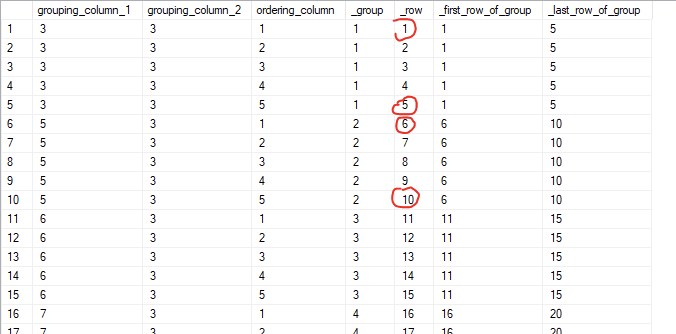
Next, we’ll chain a second CTE to calculate the first and last _row of each group. We could do this later on, but this way, we won’t have to repeat the same code and the overall result will be a little more readable.

-- continued

step_2 AS (
    SELECT *,
           MIN(_row) OVER (
                PARTITION BY _group) AS _first_row_of_group,
           MAX(_row) OVER (
                PARTITION BY _group) AS _last_row_of_group
    FROM step_1)

SELECT * FROM step_2;

Magic happens

Here’s where it starts to get interesting. Now that we have our working variables (_group, _row, _first_row_of_group and _last_row_of_group), we can start defining the “breakpoints” where we want to split into new batches.

Through some trial-and-error, I came up with the following logic:

• if the first row and the last row of a group are on each side of a row that is evenly divisible by @target_rowcount (like 100, 200, 300, etc), that first row starts a new batch.
• if the first row of a group is evenly divisible by @target_row, that first row starts a new batch.

Here’s what that looks like in T_SQL:

-- continued

step_3 AS (
    SELECT *, (CASE WHEN _row=_first_row_of_group
                     AND _first_row_of_group/@target_rowcount<
                          _last_row_of_group/@target_rowcount THEN 1
                    WHEN _row=_first_row_of_group
                     AND _first_row_of_group%@target_rowcount=0 THEN 1
                    ELSE 0
                    END) AS _increment
    FROM step_2)

SELECT * FROM step_3;

What’s up with the divisions and the modulo?

Dividing an integer in SQL Server will yield another integer – effectively the result of the division, but rounded down to the nearest integer. This actually serves us perfectly, as the integer division of a row number by the @target_rowcount is the theoretically ideal batch number for this row, if unconstrained by our grouping requirements.

The modulo operator (“%” in T-SQL) works sort of the opposite way to an integer division. Modulo gives us the remainder of a division. If a is evenly divisible by b, then the modulo, a%b, is 0. So by looking for a%b=0, we can find evenly divisible values.

4%3 is 1,
5%3 is 2,
6%3 is 0, and so on.

The column _increment can be 0 or 1, where 0 means that this group is adding to the current batch and 1 means that we’re starting a new batch. If you read the dataset from top-to-bottom, this might make a little more sense.

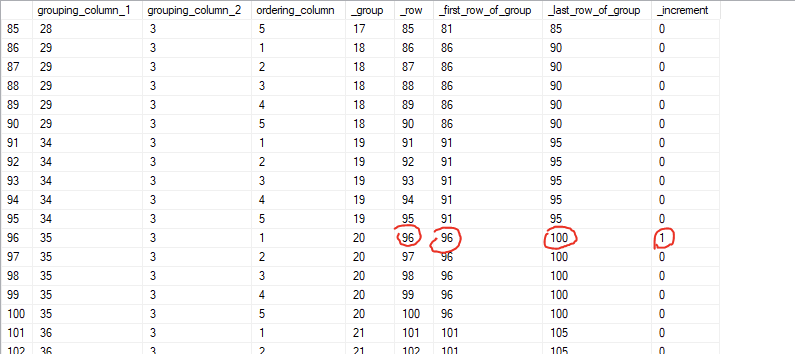
If this pattern looks familiar, it’s because it uses a similar approach as the gaps-and-islands code that Itzik Ben-Gan uses in his brilliant window function presentation.

Putting it all together

Now, all we need to do is to calculate a running total of _increment to create a batch number:

--- continued

step_4 AS (
    SELECT *, SUM(_increment) OVER (ORDER BY _row ROWS UNBOUNDED PRECEDING) AS _batch
    FROM step_3)

SELECT * FROM step_4;

When we validate the results, we can see that each batch has approximately 100 rows, depending on if the groupings allow for it.

The finished code

WITH step_1 AS (
    SELECT *,
           DENSE_RANK() OVER (
                ORDER BY grouping_column_1,
                         grouping_column_2) AS _group,
           ROW_NUMBER() OVER (
                ORDER BY grouping_column_1,
                         grouping_column_2,
                         ordering_column) AS _row
    FROM #rows),

step_2 AS (
    SELECT *,
           MIN(_row) OVER (
                PARTITION BY _group) AS _first_row_of_group,
           MAX(_row) OVER (
                PARTITION BY _group) AS _last_row_of_group
    FROM step_1),

step_3 AS (
    SELECT *, (CASE WHEN _row=_first_row_of_group
                     AND _first_row_of_group/@target_rowcount<
                          _last_row_of_group/@target_rowcount THEN 1
                    WHEN _row=_first_row_of_group
                     AND _first_row_of_group%@target_rowcount=0 THEN 1
                    ELSE 0
                    END) AS _increment
    FROM step_2),

step_4 AS (
    SELECT *, SUM(_increment) OVER (ORDER BY _row ROWS UNBOUNDED PRECEDING) AS _batch
    FROM step_3)

SELECT _batch, COUNT(*) AS row_count
FROM step_4
GROUP BY _batch
ORDER BY 1;

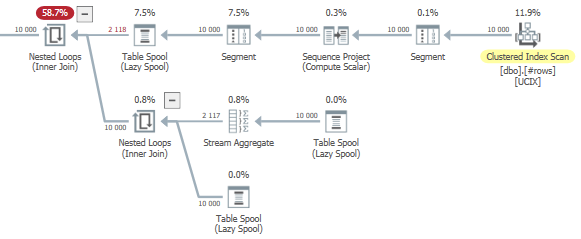
A quick look at the query plan reveals that all of these window functions quickly add some complexity.

The other thing that stands out to me is that the temp table has an index that is perfectly suited for our chain of window functions (which are all aligned by sort order), but SQL Server still introduces two Sort operations (as seen in red in the execution plan).

Obsessively tuning that last bit

Because Sort is a blocking operation, this could become noticeable if you have a much, much larger dataset, like in the millions or hundreds of millions of rows. We can fix this, but while it simplifies the plan, it will make the query a little uglier to read.

Here’s the problem: In the first CTE, we’re computing the DENSE_RANK() column _group, which we then subsequently use as our simplified grouping expression in the following CTEs. For some reason, SQL Server can’t make that leap, so it needs to sort the data stream by _group to make the window functions that depend on that column work.

Now, we can substitute “_group” for “grouping_column_1, grouping_column_2”, as well as replacing “_row” in CTE 4 with “grouping_column_1, grouping_column_2, ordering_column”, and that way we’ll maintain the same sort order throughout the entire query plan, eliminating the need for the Sort operators.

But doing that leaves the updated query looking a little more bloated:

WITH step_1 AS (
    SELECT *,
           ROW_NUMBER() OVER (
                ORDER BY grouping_column_1,
                         grouping_column_2,
                         ordering_column) AS _row
    FROM #rows),

step_2 AS (
    SELECT *,
           MIN(_row) OVER (
                PARTITION BY grouping_column_1, grouping_column_2) AS _first_row_of_group,
           MAX(_row) OVER (
                PARTITION BY grouping_column_1, grouping_column_2) AS _last_row_of_group
    FROM step_1),

step_3 AS (
    SELECT *, (CASE WHEN _row=_first_row_of_group
                     AND _first_row_of_group/@target_rowcount<
                          _last_row_of_group/@target_rowcount THEN 1
                    WHEN _row=_first_row_of_group
                     AND _first_row_of_group%@target_rowcount=0 THEN 1
                    ELSE 0
                    END) AS _increment
    FROM step_2),

step_4 AS (
    SELECT *, SUM(_increment) OVER (
        ORDER BY grouping_column_1,
                 grouping_column_2,
                 ordering_column ROWS UNBOUNDED PRECEDING) AS _batch
    FROM step_3)

SELECT *
FROM step_4;

The resulting plan looks a bit simpler, though. The Nested Loop and the Table Spool operators all relate to the windowed MIN() and MAX() functions in CTE number 2.

If I had buckets of free time and energy, that’s probably where I would try to shave off another few percent execution time.