… and what of this all has to do with IBAN numbers.

The modulus is the remainder of a division of two integers*. Suppose you divide 12 by 4, the result is 3. But divide 11 by 4, and the result is 2.75. This could also be expressed by saying that 11/4 is 2 with a remainder of 3. Computing that 3 is the work of the modulo operator, which in T-SQL is represented by the % operator.

Let’s explore how to compute the modulus of large numbers in SQL Server, and how this is useful in the real world.

Dividing integers in T-SQL will return a rounded-down integer result, known mathematically as the “quotient”:

SELECT 11.0/4 AS division,    -- 2.75
       11/4 AS quotient,      -- 2
       11%4 AS modulus;       -- 3

Modulo computations are used for a range of different applications, including computing checksums.

Dealing with very large numbers

Right out of the box, you already have some elbow room to work with large integer values in SQL Server. The bigint datatype is a signed 64-bit number, so it goes to roughly ±9.2 * 10¹⁸. If you want to go bigger than that, you can use a numeric/decimal type, which goes all the way up to ±10³⁷.

SELECT CAST(12345678901234567890123456789012345. AS numeric(38, 0))%123; -- 39

So far, the native integer types of SQL Server will do just fine.

Going bigger: manually computing the modulus

For some applications, we’ll need a way to work with numbers even larger than 37 digits. To do that, we’ll have to roll our own modulo function.

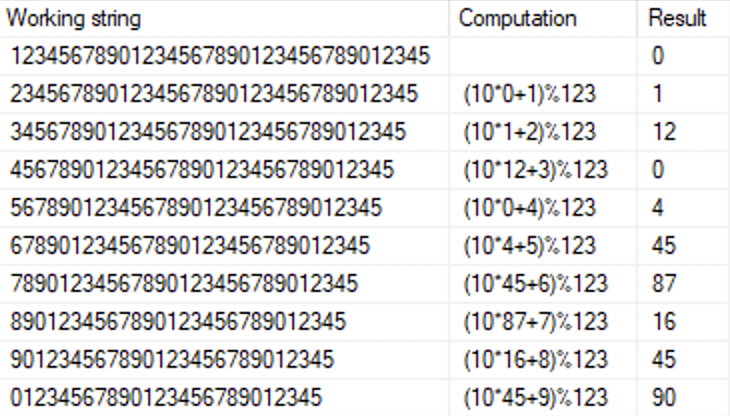
Modulo computations are kind of funny in the sense that you can iteratively compute them, one digit at a time.

We’ll define our large integer (the “dividend”) as a varchar. We’ll also define a working result variable (as an integer) that we start off at 0. For each digit in the dividend, from left-to-right, we’ll:

• multiply the previous iteration’s result by 10 (because this string is a base-10 number),
• add the left-most digit from the remaining dividend string,
• compute the modulus of this total, which becomes the new working result.

Here’s how that looks:

In T-SQL terms, this is can be expressed as a recursive common table expression:

DECLARE @bigint varchar(max)='12345678901234567890123456789012345',
        @mod int=123;

WITH bigmod AS (
    --- Starting values:
    SELECT @bigint AS working_bigint,
           0 AS working_result

    UNION ALL

    SELECT --- Truncate first character of the working input
           SUBSTRING(working_bigint, 2, LEN(working_bigint)) AS working_bigint,
           --- working_result = (10*working_result + first digit) % @mod
           (10*working_result+TRY_CAST(LEFT(working_bigint, 1) AS int))%@mod AS working_result
    FROM bigmod
    WHERE working_bigint!='')

--- Output the result of the calculation:
SELECT working_result AS modulus
FROM bigmod
WHERE working_bigint='';

Making it go faster

The recursive CTE above runs one iteration for every digit of the dividend. What if we, instead of multiplying a single digit by 10, we could capture 6 digits at a time, and multiply that number by 1,000,000?

For this to work, the length of the dividend needs to be a multiple of 6 digits, i.e. 6, 12, 18, 24, … digits. If the dividend were 17 digits, this iterative computation would not return the correct result because we’d use a 5-digit number where we’d expect a 6-digit one. To fix this, we’ll just add the required number of zeroes to the beginning of the input (where they don’t change the numeric value).

So here’s the improved code:

WITH bigmod AS (
    --- Starting values: adding 0s to the beginning to make the length evenly divisible by 6.
    SELECT REPLICATE('0', 6-(LEN(@bigint)%6))+@bigint AS working_bigint,
           0 AS working_result

    UNION ALL

    SELECT --- Truncate first 6 characters of the working input
           SUBSTRING(working_bigint, 7, LEN(working_bigint)) AS working_bigint,
           --- working_result = (10^6*working_result + first 6 digits) % @mod
           (1000000*working_result+TRY_CAST(LEFT(working_bigint, 6) AS int))%@mod AS working_result
    FROM bigmod
    WHERE working_bigint!='')

--- Output the result of the calculation:
SELECT working_result AS modulus
FROM bigmod
WHERE working_bigint='';

Let’s package this in an inline table-valued function:

CREATE FUNCTION dbo.MOD_BIG(@bigint varchar(max), @mod int)
RETURNS TABLE
WITH SCHEMABINDING
AS
 
RETURN (
    WITH bigmod AS (
        --- Starting values:
        SELECT REPLICATE('0', 6-(LEN(@bigint)%6))+@bigint AS working_bigint,
               0 AS working_result

        UNION ALL

        SELECT --- Truncate first 6 characters of the working input
               SUBSTRING(working_bigint, 7, LEN(working_bigint)) AS working_bigint,
               --- working_result = (10^6*working_result + first 6 digits) % @mod
               (1000000*working_result+TRY_CAST(LEFT(working_bigint, 6) AS int))%@mod AS working_result
        FROM bigmod
        WHERE working_bigint!='')

    --- Output the result of the calculation:
    SELECT TOP (1) working_result AS modulus
    FROM bigmod
    WHERE working_bigint='');

Validating IBAN numbers

IBAN is an international standard for denominating bank account numbers. Every country has a different way to indicate the specifics of the bank, branch, etc, but all IBAN numbers are formatted as follows:

• ANSI country code, two characters
• Check digits, two numbers
• The basic bank account number (BBAN), up to 30 characters, alphanumeric.

Here’s an example of a fictional IBAN number: MU43BOMM0101123456789101000MUR

In this case, MU is the ANSI country code for Mauritius, 43 are the check digits. The rest is the BBAN identifier.

How do the check digits work?

The check digits are computed using a MOD97 function on a number computed from the BBAN followed by the country code and 00. Any characters that are not numeric in this string need to be translated, so that A is 10, B is 11, and so on. From this resulting number (which in theory can be as long as 62 digits!) we compute the MOD97. The check digits should be (98 minus this modulus).

For our example IBAN, it will look like this:

BOMM0101123456789101000MUR MU 00

We’ll translate B to 11, O to 24, and so on:

112422220101123456789101000223027 2230 00

This number, modulo 97, is:

112422220101123456789101000223027223000%97=55

So the correct check digits should be:

98-55=43, which checks out with the original check digits we were trying to validate.

Building the number string

Just like with the modulo function, we’ll set up a recursive common table expression to replace all of the A-Z characters with numeric values. The anchor (the starting value) of the CTE

• converts all characters to upper case (just making sure),
• moves the four leading characters last in the string, and
• replaces the checksum number with a “00”.

Then, for each iteration, we’ll

• find the first occurrence of an A-Z character,
• REPLACE() all occurrences of that character in the string with its numeric representation.

The iteration is complete when there are no more A-Z characters left. The theoretical maximum number of iterations, assuming that all 25 characters exist in the string, is 25. In practice, you’d likely be looking at just a few iterations.

Here’s what that code could look like:

CREATE FUNCTION dbo.Validate_IBAN(@IBAN varchar(34))
RETURNS TABLE
WITH SCHEMABINDING
AS
 
RETURN (
    WITH acct AS (
        --- Starting value: upper case, move 4 leading characters last, replace checksum with 00.
        SELECT CAST(UPPER(REPLACE(SUBSTRING(@IBAN, 5, 100)+LEFT(@IBAN, 2), ' ', ''))+'00' AS varchar(100)) AS number_string
        UNION ALL
        --- Replace A-Z characters with number strings, 10-35:
        SELECT CAST(REPLACE(acct.number_string, x.ch, STR(ASCII(x.ch)-55, 2, 0)) AS varchar(100)) AS number_string
        FROM acct
        CROSS APPLY (
            VALUES (SUBSTRING(number_string, PATINDEX('%[A-Z]%', acct.number_string), 1))
            ) AS x(ch)
        WHERE acct.number_string LIKE '%[A-Z]%')

    --- Return what the checksum _should_ be, along with a 1/0 value if it is correct.
    SELECT TOP (1)
           REPLACE(STR(98-m.modulus, 2, 0), ' ', '9´0') AS [checksum],
           (CASE WHEN 98-m.modulus=TRY_CAST(SUBSTRING(@IBAN, 3, 2) AS int) THEN 1 ELSE 0 END) AS is_valid
    FROM acct
    CROSS APPLY dbo.MOD_BIG(number_string, 97) AS m
    WHERE acct.number_string NOT LIKE '%[A-Z]%');

Further optimizations

If you’re prepared to sacrifice readability for performance, here are some approaches I would look at:

• We’re iterating over the string twice, first when computing the numeric value of the IBAN string, then for the MOD97 operation. You could combine these two, but getting the “batching” (6 characters at a time) right may involve a few ugly code changes.
• Instead of iterating over the IBAN number, you could just write out 25 nested REPLACE() function calls, one for each character. Not as pretty, but it removes one of the recursive CTEs from the execution plan.
• In the optimized modulo function, you could process a lot more than just 6 digits at a time if you explicitly convert the working result to a larger datatype like bigint or even numeric(38, 0).
• The recursive CTEs process one IBAN number/modulo operation at a time. Batching a whole result set in the anchor of the CTE would probably make a dramatic difference if you have thousands or millions of IBAN numbers to check.

Footnotes

* For the sake of completeness, you could absolutely compute a modulus from a non-integer division. 20.4 % 2.1 = 1.5, because (20.4-1.5)/2.1=9. It’s really just a matter of moving the decimal point.

** The same solution in other programming languages: “How to compute mod of a big number?“