Probably one of the most common challenges I see when I do ETL and business intelligence work is analyzing a table (or a file) for possible primary keys. And while a bit of domain knowledge, along with a quick eye and some experience will get you really far, sometimes you may need some computational help just to be sure.
Here are some handy tricks to get you started!
Setup and scope of this post
Let’s assume we have a temp table heap called #table, with 9 columns and no indexes at all. Some columns are integers, one is a datetime and few are numeric. As I’m writing this post, my test setup has about 14.4 million rows.
In the real world, when you’re investigating a table for primary key candidates, there are a few things you’ll be looking for that are beyond the scope of this post. For instance, it’s a fair assumption that a numeric or float column is not going to be part of a primary key, varchar columns are less probable candidates than integer columns, and so on. Other factors you would take into consideration are naming conventions; column names ending with “ID” and/or columns that you can tell are foreign keys would also probably be good candidates.
In this post, I’m only looking at finding distinct values and finding the most efficient process to do so.
Initial cardinality overview
What’s the best way to see if one of the columns is completely unique? Well, if a column contains unique values, COUNT(DISTINCT column name) should be equal to COUNT(*). So let’s try that for every column in the table:
SELECT COUNT(DISTINCT TicketID) AS _dist_TicketID, COUNT(DISTINCT PassengerID) AS _dist_PassengerID, COUNT(DISTINCT ScheduleID) AS _dist_ScheduleID, COUNT(DISTINCT Departure) AS _dist_Departure, COUNT(DISTINCT SeatID) AS _dist_SeatID, COUNT(DISTINCT Fees) AS _dist_Fees, COUNT(DISTINCT Fare) AS _dist_Fare, COUNT(DISTINCT VAT) AS _dist_VAT, COUNT(DISTINCT BookingClassID) AS _dist_BookingClassID, COUNT(*) AS _count FROM #table;
On my test VM with 16 cores, this query runs for 56 CPU seconds (parallel, so it finishes in 5.8 seconds) but all those COUNT(DISTINCT) operations accumulate an eye-watering 556 MB memory grant and 170 scans totaling over a million logical reads. You’ll have guessed by now that this is a pretty expensive query.
Let’s look at the results:
![]()
We can tell from this that no single column in this table is unique, because no column has the same number of unique values as the table has rows. If we want to look at possible composite keys, of two or more columns, we’re going to look for combinations of columns whose multiplied distinct count is equal to or greater than the table’s total row count.
For example, let’s suppose that every distinct value of PassengerID exists for every distinct value of ScheduleID. That would mean that there are 308 617 x 504 = 155 million rows, so this could possibly be a composite key. However, Departure and BookingClassID cannot be a primary key candidate, because even if every possible combination of the two existed, there would only be 59 334 x 10 = 593 340 rows, which is less than the 14.4 million rows in the table.
Note that this does not prove that, say, (PassengerID, ScheduleID) is a primary key candidate, but it’s a prerequisite for finding a unique key.
Testing every composite key candidate
From the results in the example, using the multiplicational logic discussed above, I found 73 different possible composite keys to test for. Obviously, running 73 separate COUNT(DISTINCT) queries on a large table without indexes will take practically forever. So how do we test this, and what methods can we use?
Let’s look at a few different techniques to validate an example, the columns (BookingClassID, Departure, Fare).
CROSS APPLY with TOP (2)
This query is extremely fast in cases where there are plenty of duplicates. However, if the key is unique or nearly unique, it’ll run for a very long time and generate a huge number of scans (in this case, up to 14.3 million table scans at 107 000 reads each).
SELECT TOP (1) NULL
FROM #table AS t
CROSS APPLY (
SELECT TOP (2)
ROW_NUMBER() OVER (ORDER BY (SELECT NULL)) AS _rownum
FROM #table AS sub
WHERE sub.BookingClassID=t.BookingClassID AND
sub.Departure=t.Departure AND
sub.Fare=t.Fare
) AS x
WHERE x._rownum=2;
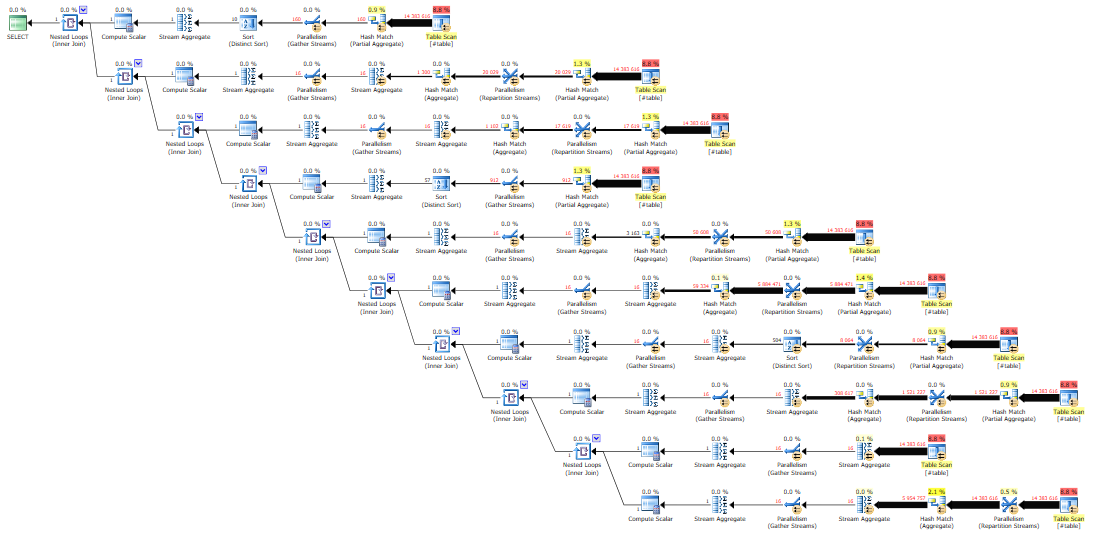
For each row in #table (“t”), we apply a Nested Loop to query the two first rows from #table (“sub”) with the same key. If we can find two rows with the same key, then those two rows are duplicates, and the query stops processing immediately. Best of all, there’s no memory grant! Here’s what the query plan looks like:

On my test rig, this query completed in less than 0.1 seconds, because it immediately found a duplicate record.
GROUP BY with HAVING COUNT(*)
This is the simple approach and the true generalist. The query aggregates all of the rows in the table using a memory-hungry Hash Match (aggregate) and then filters the result for rows where COUNT(*)>1. The execution time and the number of reads will be the same whether or not the candidate key is unique or not.
SELECT TOP (1) NULL FROM #table GROUP BY BookingClassID, Departure, Fare HAVING COUNT(*)>1;
Because of the Hash Match (aggregate), and because it needs to go through the entire table, this query runs up a pretty awesome memory grant, some 1.3 GB on my system. If you share your server with others, you’ll want to put a leash on that puppy.

When running fully parallel on 16 threads, it completes in 1.4 seconds, as opposed to 13 seconds when serial. This solution is very similar with regards to query plan and performance to a plain SELECT DISTINCT with a COUNT(*):
SELECT COUNT(*) --- will be equal to the total number --- of rows in #table if the key is unique. FROM ( SELECT DISTINCT BookingClassID, Departure, Fare FROM #table ) AS sub;
Adding an IDENTITY and a clustered index
You can improve on the CROSS APPLY solution by adding an IDENTITY() column when you create/load the temp table, which you use to create a unique, clustered index. This takes a bit of time, but you only have to do it once, because it can be re-used over and over.
ALTER TABLE #table ADD _id int IDENTITY(1, 1) NOT NULL; CREATE UNIQUE CLUSTERED INDEX CIX ON #table (_id);
Now, with the table clustered on this identity column, we can redesign the CROSS APPLY query to use a clustered seek operator (a range scan) instead of a complete table scan. This can dramatically reduce the I/O.
SELECT TOP (1) NULL
FROM #table AS t
CROSS APPLY (
SELECT TOP (1) NULL AS n
FROM #table AS sub
WHERE sub.BookingClassID=t.BookingClassID AND
sub.Departure=t.Departure AND
sub.Fare=t.Fare AND
sub._id>t._id
) AS x;
Note the “sub._id>t._id”, the “TOP (2)” that we’ve changed into “TOP (1)”, and that we’ve removed the ROW_NUMBER() function. The query plan still looks similar to before, but a lot simplified.
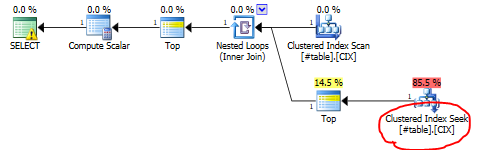
Down from the previous 0.1 seconds, this query now runs in just two milliseconds, which is an effect of the much more efficient seek. But remember that this solution is still vastly slower than the GROUP BY with COUNT(*) solution when a key is unique or nearly unique. With a unique candidate key, this query can still easily run for hours.
An iterative sample approach
Some of the composite key candidates are obvious duplicates if you look at just a small sample of the table, so we can build an iterative procedure that tests increasingly large samples of data until it either finds a duplicate record or scans the entire table and concludes the composite key to be unique.
Looking at the GROUP BY with COUNT(*) approach we tried above, here’s how an iterative test could look:
DECLARE @sample int=1000, @duplicates bit=0; DECLARE @rowcount int=(SELECT COUNT(*) FROM #table); --- Keep going until a) we find a duplicate record, or --- b) the sample size covers the entire table. WHILE (@duplicates=0 AND @sample<@rowcount) BEGIN; --- Increase the sample size for each run: SET @sample=@sample*5; --- If we find a duplicate, set @duplicates=1. SELECT TOP (1) @duplicates=1 FROM ( SELECT TOP (@sample) * FROM #table ) AS t GROUP BY BookingClassID, Departure, Fare HAVING COUNT(*)>1; END; SELECT @duplicates AS [Duplicates found], @sample AS [Sample size];
We’ll just try the first 5 000 rows to begin with. If that doesn’t return a duplicate row, try 25 000 rows, then 125 000 rows and so on. You could probably scale up the sample size as much as you want – I haven’t really tested if 5 times is an optimal number.
Testing samples quickly eliminates most of the candidates, so you can focus your computing power on the near-unique candidates. And the smaller datasets keep your memory grants nice and small. With my sample data, I found a duplicate among the first 5 000 rows, so this test ran for a total of only 8 milliseconds, excluding the COUNT(*) at the top.
Have you done this kind before?
I hear you. If this is all a bit rich for you, there’s a stored procedure that pretty much does all this stuff for you. The usual disclaimer applies, though: don’t just run code that you got from a stranger on the Internet. Please review and test it first. If it’s free, it’s on you. Have fun!