T-SQL math patterns

As part of spending waaaaaay to much time trying to solve the 2023 Advent of Code challenges, I came across multiple instances where I had to dust off some old math that I hadn’t paid attention to since I went to school back in the 90ies.

So for my own convenience, and yours, I’ve built functions for some common math that you might perhaps encounter at some point. I found this whole experience to be a great way to familiarize myself with a lot of the new functionality in SQL Server 2022, including GENERATE_SERIES(), LEAST(), GREATEST() and more. The Github repo contains a SQL Server 2019 version where I’ve built drop-in versions of the 2022 functions, but they probably won’t perform as well as the built-in stuff.

If there are any other functions you’d like to add, feel free to add a comment to this post, or, by all means, a pull request to the repo.

Prime numbers

Prime numbers are integers that are not evenly divisible by any other integer than themselves and 1. This means that every positive integer can be expressed as the multiple of one or more primes. For instance, 18 is the product of the prime numbers 2, 3, and 3. Those prime factors, in turn are useful for computing things like the least common multiple of two or more integers.

Computing prime numbers is potentially long-running iterative work. It’s not rocket science, it’s just that there’s no algorithmically “smart” way to do it other than just trying every combination and see what comes out.

Luckily, the GENERATE_SERIES() function makes coding a prime number function pretty short work.

--- All primes up to 10,000
SELECT prime FROM Math.Primes(10000);

Prime factors

This function computes all the prime factors that make up an integer.

To compute the prime factors of an integer, we’ll use a recursive common table expression with two columns; the prime and the remainder. For each iteration of the CTE, we’ll divide the remainder by the smallest prime we can find that it is evenly divisible by, and add that prime number to the list.

Here’s what the CTE looks like:

    WITH rcte AS (
        SELECT CAST(1 AS bigint) AS prime,
               CAST(@integer AS bigint) AS remain
        --- Keeping it real:
        WHERE @integer>0

        UNION ALL

        SELECT p.prime,
               rcte.remain/p.prime AS remain
        FROM rcte
        CROSS APPLY (
            SELECT prime
            FROM (
                --- The ROW_NUMBER() pattern is a workaround because recursive
                --- common table expressions cannot contain TOP()
                SELECT p.prime, ROW_NUMBER() OVER (ORDER BY p.prime) AS _rn
                FROM Math.Primes(rcte.remain) AS p
                --- Only look at primes that are equal to or larger than
                --- the ones we've already found:
                WHERE p.prime>=rcte.prime
                  AND rcte.remain%p.prime=0
                ) AS x
            WHERE _rn=1
            ) AS p
        --- Continue the recursion until we've exhausted all the
        --- prime factors:
        WHERE rcte.remain!=1)

    SELECT prime
    FROM rcte
    WHERE prime>1

Fun sidenote: SQL Server does not allow TOP and ORDER BY in the recursive part of a CTE, so in order to return just the TOP (1) prime from our CROSS APPLY, I used a ROW_NUMBER() function, which I could then filter by. Often, a ROW_NUMBER() that is filtered is actually made into a Top operator in the query plan once the query is optimized by SQL Server.

--- All the primes that, when multiplied together, make up the number 12,345,678:
SELECT prime FROM Math.Prime_factors(12345678);

Greatest common divisor (gcd)

The greatest common divisor (the GCD) is the largest positive integer that divides each of the integers. I honestly don’t have the math chops to accurately account for how it’s used outside of discrete mathematics, but it can also be used to compute the least common multiples of two numbers, which has more tangible, real-world applications.

For this function, I’ve used the Euclidean algorithm, as it is computationally the most efficient one I would make into T-SQL.

    WITH cte AS (
        SELECT GREATEST(@a, @b) AS a, LEAST(@a, @b) AS b

        UNION ALL

        SELECT b AS a, a%b AS b
        FROM cte
        WHERE b!=0
    )

    SELECT @res=a
    FROM cte
    WHERE b=0;

Here’s how to use the function:

--- Compute the greatest common divisor of 1,071 and 462:
SELECT Math.Greatest_common_divisor(1071, 462);

Least common multiple (lcm)

The least common multiple helps you compute cyclic recurrences. Imagine, for instance, that you have three revolving contracts with different term lengths. One renews every three months, the other renews every two months and a third renews every five months. The least common multiple of (3, 2, 5) tells you which month all three contracts renew at the same time.

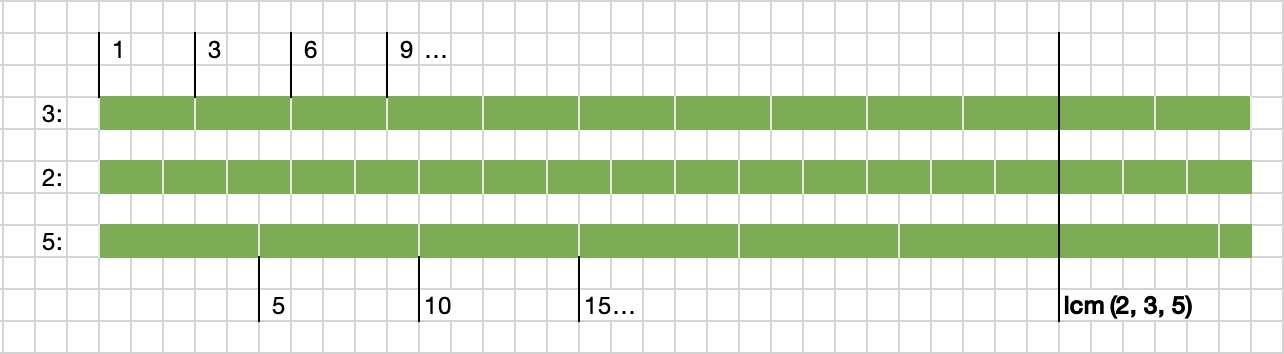
The least common multiple can be computed in a number of ways. The easiest way is to determine the greatest common divisor, because the gcd(a, b) * lcm(a, b) = |a * b|, so we can just take the gcd and divide it by the absolute of the product of the two factors.

        SELECT ABS(@a*@b)/Math.Greatest_common_divisor(@a, @b)

Because I’m not sure how this translates when you use more than two integer inputs, I’ve also created a version based on prime factorization.

--- Using the gcd, this function is very efficient:
SELECT Math.Least_common_multiple(1071, 462);

--- This function uses prime factorization, which makes it slower,
--- but you can add as many numbers as you like
SELECT Math.Least_common_multiple_using_primes('1071, 462');

Finding the roots of a quadratic polynomial

A quadratic polynomial, or a parabolic function, is a function that looks like this:

y(x) = ax2 + bx + c

The two points where the line crosses the x axis are known as the “roots” of the function. In an optmization scenario, you may want to find the interval in which the function is above or below zero (depending on if a is positive or negative). You could do this by just trying every value of x, but this is an expensive, iterative approach that could take a long time and generate rather imprecise results.

A better way is to algorithmically compute the roots, using a method called “completing the square“. I hated this at school, because I could never commit it to memory, but the good news is that I have my T-SQL next time I need it.

Here’s how to find the roots with the T-SQL function:

--- Find the roots for 0.3x2 + 2x -4 = 0
SELECT x FROM Math.Parabolic_roots(0.3, 2, -4);

Factorials

If you have four cars to park in four slots, how many ways could you park them? You could park any of four different cars in the first slot. After that, you can choose any one of the three remaining cars for the second slot, leaving you with one of two for the third slot, and just a single car for the fourth slot. Expressed mathematically, you have 4*3*2*1 unique ways of parking the four cars in the four slots. This calculation usually expressed with an exclamation point, a “bang” and is know as “4 factorial”:

4! = 4 * 3 * 2 * 1

I built a function that does this for you, mostly as a helper function, as factorials are useful in combinatorics and probability calculations.

--- Compute 24!
SELECT Math.Factorial(24);

How to aggregate a set of numbers with multiplication

You can easily add a large number of values using the SUM() aggregate function in T-SQL, but there’s no equivalent function for multiplying all the values from a set. But if you remember 9th grade math, you’ll realize that

log10(a)+log10(b) = log10(a*b)

=> 10^( log10(a)+log10(b) ) = a*b

… or, expressed in T-SQL:

SELECT EXP(SUM(LOG(n))) -- returns the multiple of all n

This allows us to build a really compact and good-looking factorial function:

        SELECT CAST(ROUND(EXP(SUM(LOG(CAST([value] AS numeric(38, 18))))), 0) AS numeric(38, 0))
        FROM GENERATE_SERIES(1, @n, 1)

n over k

Back to the example of parking cars. What if you have four cars and seven parking slots to park them in. In combinatorics, there are “n over k”, or 7 over 4, ways to assign these cars to parking slots:

SELECT Math.nCk(7, 4);

In mathematical terms, n over k is

n! / (k!(n-k)!)