Catching circular references in parent-child structures

A popular form of organizing dimensions is in parent-child structures, also known as “unbalanced” or “ragged” dimensions, because any branch can have an arbitrary number of child levels. There are many advantages to this type of representation, but their recursive nature also brings some challenges. In this post, we’re going to look at circular references, and how you can trap them before they run out of control.

Suppose you have a tree hierarchy where (among other members) “3” is the parent of “8”, “8” is the parent of “B” and “B” is the parent of “E”. You could easily draw this as a branch structure where the members could be profit centers of a company, divisions of government, managers and employees, product lines, cell references in an Excel sheet or pretty much anything that can be described as a hierarchy.

3
--8
  --B
    --E

Now, if we say that “E” is the parent of “3”, we’ve created a circular reference, and we end up with an infinite recursion. What that means is that if you follow the tree from the root to the leaf level, you’ll end up going round and round in circles. In terms of a database query, that means that the query will go on forever until it either fills up your log file or tempdb, or until the maximum number of recursions (OPTION MAXRECURSION) is reached, whichever happens first.

The error message will look something like this:

Msg 530, Level 16, State 1, Line 1
The statement terminated. The maximum recursion 100 has been exhausted before statement completion.

And that’s not a problem – you could trap this error using a TRY-CATCH block, but that won’t show you the actual circular reference in your table that you need to fix for your fancy hierarchy to work.

Some test data

Let’s create a temp table with some 14 000 rows in a parent-child structure.

CREATE TABLE #table (
    id        int NOT NULL,
    name      varchar(10) NOT NULL,
    parent    int NULL,
    PRIMARY KEY CLUSTERED (id)
);

CREATE UNIQUE INDEX IX_table_parent
    ON #table (parent, id)
    INCLUDE (name);

--- Add 14 000 rows to the table:
INSERT INTO #table (id, name, parent)
SELECT x.n+v.id, v.name, x.n+v.parent
FROM (
    SELECT TOP (999)
           100000*ROW_NUMBER() OVER (ORDER BY (SELECT NULL)) AS n
    FROM sys.columns
    ) AS x
CROSS JOIN (
    VALUES (1,  '1', NULL), (2,  '2', 1),
           (3,  '3', 14),   (4,  '4', 1),
           (5,  '5', 2),    (6,  '6', 2),
           (7,  '7', 3),    (8,  '8', 3),
           (9,  '9', 5),    (10, 'A', 7),
           (11, 'B', 8),    (12, 'C', 9),
           (13, 'D', 10),   (14, 'E', 11)
    ) AS v(id, name, parent);

--- Intentionally create a circular reference:
UPDATE #table SET parent=700014 WHERE id=700003;

Finding the recursion

If you’re new to recursive common table expressions, this next part is not going to make any sense at all to you, so go ahead and read up on that first.

The plan for our query is simple enough. Start with an anchor row (any row can be an anchor), and from that row, find its children, their children, etc until we either reach the leaf level – or until we get back to the anchor again. If we reach the leaf level, all is fine. If we come back to the anchor, we’ve found a circular reference. Then we’ll want to have a trail of “breadcrumbs”, a path, of how we got there.

Break any one of those links in that path, and you’ve resolved the circular reference.

Let’s look at all the pieces one at a time.

The anchor

    SELECT parent AS start_id,
           id,
           CAST(name AS varchar(max)) AS [path]
    FROM #table

Every row is a potential anchor. In this result set, we have three columns. The “start_id” is the id of the anchor row, which we’ll keep throughout the recursion. Whenever our recursion returns to “start_id”, we’ve found a circular reference.

“id” is the current row of the recursion. It starts as the child of “start_id”, then its grandchild, great grandchild, and so on.

“path” is a textual representation, our trail of breadcrumbs. This will be used to show a human reader how a potential circular reference happened.

The recursion

    SELECT rcte.start_id,
           t.id,
           CAST(rcte.[path]+' -> '+t.name AS varchar(max)) AS [path]
    FROM rcte
    INNER JOIN #table AS t ON
        t.parent=rcte.id
    WHERE rcte.start_id!=rcte.id

The recursion finds all children of “id”, thereby traversing the tree towards the leaf level. “start_id” stays the same (it’s our anchor), “id” is the new child row, and we’re adding plaintext breadcrumbs to the end of the “path” column.

This recursion will end when there are no more children available, which means that we’ve reached the leaf level.

But we also need it to stop if we were to find a circular reference, and that’s why we’ve added that last WHERE clause. When “id” is “start_id”, we’ve gone full circle, and it’s time to pull on the brakes.

The complete solution

Putting it all together, here’s the final product:

WITH rcte AS (
    --- Anchor: any row in #table could be an anchor
    --- in an infinite recursion.
    SELECT parent AS start_id,
           id,
           CAST(name AS varchar(max)) AS [path]
    FROM #table

    UNION ALL

    --- Find children. Keep this up until we circle back
    --- to the anchor row, which we keep in the "start_id"
    --- column.
    SELECT rcte.start_id,
           t.id,
           CAST(rcte.[path]+' -> '+t.name AS varchar(max)) AS [path]
    FROM rcte
    INNER JOIN #table AS t ON
        t.parent=rcte.id
    WHERE rcte.start_id!=rcte.id)

SELECT start_id, [path]
FROM rcte
WHERE start_id=id
OPTION (MAXRECURSION 0);    -- eliminates "assert" operator.

That MAXRECURSION hint is there to simplify the plan. You trust me, right?

Here’s the output from the sample data.

start_id    path
----------  --------------------
700014      3 -> 8 -> B -> E
700011      E -> 3 -> 8 -> B
700008      B -> E -> 3 -> 8
700003      8 -> B -> E -> 3

You may notice that it’s actually the same recursion, represented in four different ways. You could argue that this is by design, or you could spend time trying to eliminate the “duplicates” of the chain.

The query plan

Thanks to some optimal indexing, we’ve found a very efficient plan, with zero memory grant and no blocking operators.

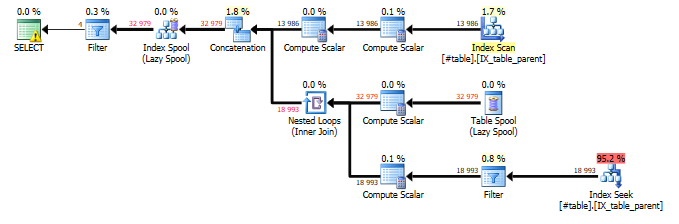
Here’s how to read the plan: For the sake of brevity, you can completely ignore the Compute Scalar operators, which are just scalar operations like string parsing, incrementing counters, etc.

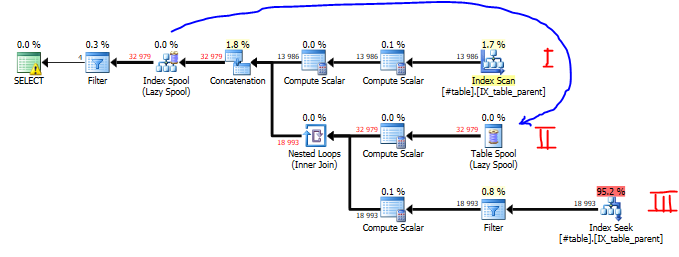
I: The Index scan collects all the anchors of the query. The anchor rows move left in the diagram until they’re stored in an Index Spool, which is kind of an internal high-performance temp table.

II: The rows that were just stored in the Spool are then retrieved, and joined…

III: … using an Index Seek (finding rows that are children of each row from II). The filter operator then makes sure to eliminates rows where “start_id” is equal to “id” (corresponding to the WHERE clause in the recursive part).

This whole process generates even more rows that are moved into the Index Spool, and the process repeats itself over and over, until there are no more recursions. Finally, the top-left Filter operator isolates only rows where “id” equals “start_id”, so we only see just the circular references we’re looking for.

Indexing

Making a recursive query like this run smoothly relies on an index on (parent_id, id). This allows the Nested Loop operator in the recursive part of the CTE to issue an Index Seek on all rows with a specific “parent_id”, rather than having to scan through the entire table looking for matching children.

Remember that Nested Loop Join means that anything that happens “below” the operator in the graphical plan is performed once for each row, so performance here is key.