A faster Fibonacci series in T-SQL

Fibonacci’s numbers are a sequence of numbers calculated using a recursion pattern that typically lends itself more to procedural programming. This makes it trickier to implement in a well-performing solution in T-SQL, as T-SQL is set-based.

The calculation in itself is really simple: each value is calculated from the sum of the previous two values:

0 + 1   = 1
1 + 1   = 2
1 + 2   = 3
2 + 3   = 5
3 + 5   = 8
5 + 8   = 13

The recursive common table expression

This is the solution that probably comes to mind first. A recursive common table expression iterates through the series in a procedural manner.

WITH rcte ([count], n1, n2)
AS (
    --- Starting values (the anchor)
    SELECT 1 AS [count],
           CAST(0 AS numeric(38, 0)),
           CAST(1 AS numeric(38, 0))
    UNION ALL
    --- The recursion:
    SELECT [count]+1,
           n2,
           n1+n2
    FROM rcte
    WHERE [count]<183)

SELECT n2 FROM rcte
OPTION (MAXRECURSION 0);

Not the prettiest execution plan, but it’s non-blocking and efficient:

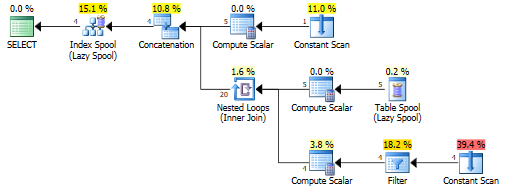
Fibonacci, recursive CTE

This solution just requires two constants (0 and 1) as starting values, so you don’t need temp tables, which is nice.

The quirky update

A different approach is the infamous quirky update, where you can update variables inline in a regular UPDATE statement. For this to work, we’ll need to set up a work table to play with:

SELECT TOP 200 CAST(NULL AS numeric(38, 0)) AS n
INTO #work
FROM master..spt_values;

With the work table set up, we can run a single-pass update statement on the table that effectively loops through all of the rows:

DECLARE @n1 numeric(38, 0)=0,   -- Starting value
        @n2 numeric(38, 0)=1,   -- Starting value
        @n3 numeric(38, 0);

UPDATE TOP (182) #work
SET @n3=@n1+@n2,   -- Variable assignment
    @n1=@n2,       -- Variable assignment
    @n2=@n3,       -- Variable assignment
      n=@n3;       -- Set column value to @n3

SELECT *
FROM #work
WHERE n IS NOT NULL;

Important to note with quirky updates is that there is no guarantee as to the processing order of the rows. In this calculation, however, this won’t matter because we don’t read anything from the table in the operation.

The execution plan for the quirky update is a showcase of sheer simplicity:

Fibonacci, quirky update

What about a cursor?

Let’s not.

Using maths

There’s a really nice mathematical way that I found on Stack Overflow, using the golden ratio (from Wikipedia). And it’s actually set-based. I don’t have the requisite mathematical skills to evaluate the correctness or precision. Note that it returns a float value result, the upside of which is that you can calculate much higher values. The downside is the loss of precision that comes with float.

SELECT FLOOR(
             POWER((1+SQRT(5))/2.0, number)/
             SQRT(5)+0.5
            )
FROM master..spt_values
WHERE [type]='P' AND
      number BETWEEN 1 AND 182;

Performance

The largest integer datatype in SQL Server, numeric(38, 0), only allows for some 182 iterations of the Fibonacci series, so there’s really nothing to measure. In a different operation where you would have thousands or millions of iterations, the quirky update is probably faster (if applicable), but it always comes down to the specifics of your query.